Algoritmo de Huffman
Hola en esta entrada hablaré sobre el algoritmo de Huffman, este algoritmo se usa precisamente para construir códigos de Huffman, lo que hace es tomar un alfabeto de n símbolos, también toma las frecuencias para cada símbolo, luego produce un código de Huffman con estos elementos.
El objetivo de construir códigos de Huffman es el de la compresión de datos, es decir, expresar de una manera distinta (más corta, obviamente) la misma información.
A continuación explicaré a detalle el funcionamiento del algoritmo.
Vamos a obtener el código de Huffman de la palabra: "ingeniero".
Lo primero a realizar es obtener las frecuencias de cada elemento de la sentencia, es decir, las veces que aparece cada caracter en nuestra palabra u oración, dependiendo el caso.
En nuestro caso quedaría de la siguiente manera.
Lo siguiente es ordenar estos caracteres en función a las frecuencias obtenidas, de menor a mayor y dejándo solo el caracter con su correspondiente frecuencia, quedaría de la siguiente manera.
Lo siguiente es la construcción de un árbol binario mediante la unión de nodos que contienen el caracter y su respectiva frecuencia, los nodos que tenemos hasta ahorita son los siguientes.
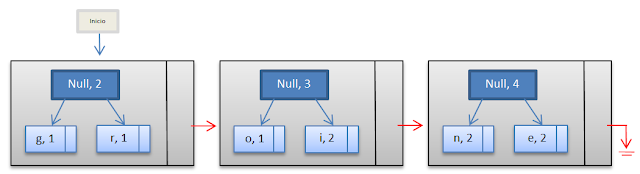
Ahora lo que toca hacer es ir uniendo los nodos consecutivos en pares, sumaremos las frecuencias de esos dos nodos y luego con ellos crearemos un nuevo nodo. El nuevo nodo contendrá un caracter "null", seguido de la frecuencia obtenida al sumar las 2 frecuencias de los nodos con que se formó. Para entender mejor el concepto realizaremos este paso con los primeros 2 nodos de nuestro conjunto. El resultado es el siguiente.
Lo primero a realizar es obtener las frecuencias de cada elemento de la sentencia, es decir, las veces que aparece cada caracter en nuestra palabra u oración, dependiendo el caso.
En nuestro caso quedaría de la siguiente manera.
Lo siguiente es ordenar estos caracteres en función a las frecuencias obtenidas, de menor a mayor y dejándo solo el caracter con su correspondiente frecuencia, quedaría de la siguiente manera.
Lo siguiente es la construcción de un árbol binario mediante la unión de nodos que contienen el caracter y su respectiva frecuencia, los nodos que tenemos hasta ahorita son los siguientes.
Ahora lo que toca hacer es ir uniendo los nodos consecutivos en pares, sumaremos las frecuencias de esos dos nodos y luego con ellos crearemos un nuevo nodo. El nuevo nodo contendrá un caracter "null", seguido de la frecuencia obtenida al sumar las 2 frecuencias de los nodos con que se formó. Para entender mejor el concepto realizaremos este paso con los primeros 2 nodos de nuestro conjunto. El resultado es el siguiente.
Noten que ahora el inicio es de nuestra lista es otro, ahora está al inicio el tercer nodo que teníamos en nuestra lista anterior, los nodos que retiramos ahora se encuentran dentro del nuevo nodo que formamos con la suma de sus respectivas frecuencias. El nuevo nodo es colocado al final de la lista.
Ahora, si seguimos el mismo procedimiento podemos concluir que obtendremos un árbol binario, donde las hojas del mismo serán los caracteres de nuestra palabra. Al seguir realizando el mismo procedimiento obtendremos lo siguiente.
Luego.
Hacemos el mismo procedimiento con los nodos nuevos, se crea un nodo nuevo con la suma de las frecuencias, y le antecede un null.
Ahora, si seguimos el mismo procedimiento podemos concluir que obtendremos un árbol binario, donde las hojas del mismo serán los caracteres de nuestra palabra. Al seguir realizando el mismo procedimiento obtendremos lo siguiente.
Luego.
Hacemos el mismo procedimiento con los nodos nuevos, se crea un nodo nuevo con la suma de las frecuencias, y le antecede un null.
Al final queda un árbol binario de la siguiente manera.
Lo siguiente es asignar ceros y unos a las ramas del árbol, las de la izquierda serán ceros, mientras que las de la derecha serán unos.
Mediante esta asignación de números podemos determinar el camino para llegar al caracter deseado, por ejemplo si queremos llegar a n, el recorrido es 00, mientras que para e, el recorrido es 01. Podemos hacer lo mismo para obtener el código de las demás letras de nuestra palabra, a continuación muestro una tabla con los caracteres, su frecuencia y su código de Huffman correspondiente a esta palabra.
Yo implementé el algoritmo de Huffman en python, el siguiente es el código fuente:
Y este es el resultado de la ejecución del script.
Para "hello huffman":
Para "arsenal fc"
Para "Facultad de Ingenieria Mecanica y Electrica"
Para medir la efectividad de compresión de datos por el algoritmo de Huffman partimos de la idea de la equivalencia de un caracter y un byte, es decir el largo de caracteres de la cadena introducida será el valor de bytes de la misma, seguido de eso podemos obtener el valor de bytes después de la compresión, dividiendo la cadena binaria obtenida entre 8.
Por último imprimí también la relación entre la entrada y salida, quedando los resultados de la siguiente manera:
El resultado es una compresión de cerca del doble.
Veamos ahora con cadenas más largas.
Podemos observar nuevamente que la relación es cercana al doble, tomando en cuenta que existe un mayor número de caracteres.
Es todo por esta entrada. Cualquier duda o aclaración pueden dejarla en comentarios.
Bibliografía:
http://www.alegsa.com.ar/Diccionario/C/1048.php
https://www.youtube.com/watch?v=8Gf8wutvS1w
Liga hacia mi git: https://github.com/eddypre/M-todosCodificaci-n
Lo siguiente es asignar ceros y unos a las ramas del árbol, las de la izquierda serán ceros, mientras que las de la derecha serán unos.
Mediante esta asignación de números podemos determinar el camino para llegar al caracter deseado, por ejemplo si queremos llegar a n, el recorrido es 00, mientras que para e, el recorrido es 01. Podemos hacer lo mismo para obtener el código de las demás letras de nuestra palabra, a continuación muestro una tabla con los caracteres, su frecuencia y su código de Huffman correspondiente a esta palabra.
Yo implementé el algoritmo de Huffman en python, el siguiente es el código fuente:
'''
Algoritmo de Huffman
Compresion de datos
'''
def huff():
text = raw_input("Put your text: ")
let = dict()
large1 = len(text)
for i in range (large1):
if text[i] in let:
let[text[i]] += 1
else:
let[text[i]] = 1
k = let.items()
large2 = len(k)
for i in range(large2):
men = k[i][1] #menor
for j in range(len(k)):
if k[j][1] > men:
men,let2 = k[j][1],k[j][0]
a,b = k[i][1],k[i][0]
k[j] = (b,a)
k[i] = (let2,men)
num = []
lett = []
comb = []
for i in range(len(k)):
num.append(k[i][1])
lett.append(k[i][0])
comb.append((k[i][0],0,0))
tam = 0
#Finish - tree
size = len(num)
while (len(num) > 1):
m = num[0] #
z = 0
a = lett[0]
for i in range(len(num)):
if num[i] < m:
m = num[i]
a = lett[i]
z = i
lett.pop(z)
num.pop(z)
mini = num[0]
j = 0
b = lett[0]
for i in range(len(num)):
if num[i] < mini:
mini = num[i]
b = lett[i]
j = i
add = m + mini
lett[j] = tam
num[j] = add
comb.append((tam,0,0))
if m >= mini:
counter = 1
con = 0
else:
counter = 0
con = 1
for q in range(len(comb)):
if comb[q][0] == a:
comb[q] = (a,counter,tam)
if comb[q][0] == b:
comb[q] = (b,con,tam)
tam += 1
#Finish1
num = [] #
leng = len(comb)
last = comb[leng-1][0]
k = 0
for i in range(size):
num.append([])
a,b,c = comb[i]
num[i].append(str(b))
q = i
cont = 0
while(q <= leng-2):
if(comb[q][0] == c):
c = comb[q][2]
num[i].append(str(comb[q][1]))
cont = c
if cont == last:
break
q += 1
num[i] =num[i][::-1]
#Finish2-
code = []
for i in range(len(text)):
last = 0
while (last <= size):
if comb[last][0] == text[i]:
break
last += 1
cads = "".join(num[last])
code.append((cads))
#print "Code: ",code
new = []
for i in range(len(code)):
new.append(str(code[i]))
new = "".join(new)
cal = []
j, k, i, l = 0,0,0,0 #another
temp = []
while(i < len(new)):
l = 1
j = 0
while(j < len(num) ):
k = 0
if new[i] == num[j][k]:
k += 1
if len(num[j]) == k:
l = k
temp.append(comb[j][0])
while (k < len(num[j])):
if new[i+k] == num[j][k]:
k += 1
if k == len(num[j]):
temp.append(comb[j][0])
l = k
else:
k = len(num[j])
j += 1
i += l
lenew = len(new)
trans = "".join(temp)
print "Binary: ",new
#print "Code: ",code
print "Translate: ",trans
print "\nLength of text: ", large1
print "In bytes: ", large1
bytecomp = float(lenew/8.0)
print "Bytes affter compression: ", bytecomp
print "Relation: ", float(large1/bytecomp)
if __name__ == '__main__':
huff()
Y este es el resultado de la ejecución del script.
Para "hello huffman":
Para "arsenal fc"
Para "Facultad de Ingenieria Mecanica y Electrica"
Para medir la efectividad de compresión de datos por el algoritmo de Huffman partimos de la idea de la equivalencia de un caracter y un byte, es decir el largo de caracteres de la cadena introducida será el valor de bytes de la misma, seguido de eso podemos obtener el valor de bytes después de la compresión, dividiendo la cadena binaria obtenida entre 8.
Por último imprimí también la relación entre la entrada y salida, quedando los resultados de la siguiente manera:
El resultado es una compresión de cerca del doble.
Veamos ahora con cadenas más largas.
Podemos observar nuevamente que la relación es cercana al doble, tomando en cuenta que existe un mayor número de caracteres.
Es todo por esta entrada. Cualquier duda o aclaración pueden dejarla en comentarios.
Bibliografía:
http://www.alegsa.com.ar/Diccionario/C/1048.php
https://www.youtube.com/watch?v=8Gf8wutvS1w
Liga hacia mi git: https://github.com/eddypre/M-todosCodificaci-n
Saludos!














El reporte no corresponde a lo que se esperaba de análisis de casos peor versus típico... 7+4 pts.
ResponderEliminar